본 게시물의 전문은 chatgpt 기반의(언어모델 : gpt 4o) 답변임을 알려드립니다.
Disjoint Set 자료구조는 연결 성분 탐색과 같은 그래프 알고리즘에서 효과적으로 사용됩니다. 각 노드가 속한 집합을 빠르게 찾고, 집합을 병합함으로써 효율적인 그래프 탐색이 가능합니다.
1. Disjoint Set (서로소 집합) 자료구조
- 개념:
Disjoint Set 자료구조는 서로 겹치지 않는 여러 집합들을 관리합니다.
이 자료구조는 집합 간 교집합 없이 독립적인 집합의 모음을 유지합니다. - 기본 연산:
- make-set(x):
- 새로운 집합을 생성하고, 원소 x를 그 집합의 멤버로 추가합니다.
- ex) {x} 형태로 집합 생성.
- find-set(x):
- 원소 x가 속한 집합의 대표 원소(대표자)를 반환합니다.
- 대표자는 해당 집합을 구분하는 식별자 역할을 합니다.
- 모든 멤버는 대표자가 될 수 있음.
- union(x, y):
- 두 집합을 병합하여 하나의 집합으로 만듭니다.
- 이때 두 집합의 대표자가 달라지는 경우 갱신이 필요합니다.
- ex) {x}, {y} → {x ∪ y}
- make-set(x):
- 적용 예시: Prim’s Algorithm, Kruskal’s Algorithm과 같은 최소 신장 트리 알고리즘에서 사용됩니다.
2. Disjoint Set을 활용한 연결 성분(Connected Components) 탐색
- 연결 성분 (Connected Components):
- 정의:
그래프 G의 연결 성분은 그래프의 부분 그래프(subgraph)로,
그 안의 모든 노드 쌍이 서로 경로로 연결된 집합입니다. - 노드 사이에 경로가 존재하는 경우 같은 연결 성분에 속합니다.
- 즉, 입력이 무향그래프
- 정의:
- 연결 성분 찾기:
- Disjoint Set 자료구조를 활용하여 무방향 그래프의 연결 성분을 찾을 수 있습니다.
- 그래프의 각 노드에 대해 find-set과 union 연산을 반복하여 서로 연결된 노드들을 동일한 집합으로 병합합니다.
- 예제:
- 주어진 그래프 G에서 두 개의 연결 성분 발견:
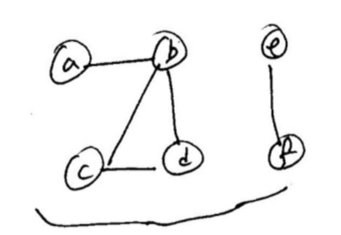
- {a, b, c, d}
- {e, f}
3. Connected Components 알고리즘
Disjoint Set 자료구조를 이용해 그래프의 연결 성분(Connected Components)을 찾는 알고리즘과 응용을 설명합니다. 이 알고리즘은 각 정점의 소속 집합을 관리하면서 서로 다른 연결 성분을 병합(Union)하여 최종 연결 성분을 찾습니다.
알고리즘 흐름:

입력:
- 무방향 그래프 G = (V, E)
- V: 정점 집합
- E: 간선 집합
절차:
- 모든 정점에 대해 make-set(v) 실행:
- 각 정점 v를 독립적인 집합으로 초기화합니다.
- 모든 간선(u, v)에 대해 탐색:
- find-set(u)와 find-set(v)로 두 정점의 대표자를 찾습니다.
- 만약 두 대표자가 다른 집합에 속하면 union(u, v)를 통해 두 집합을 병합합니다.
이 과정을 통해, 서로 연결된 정점들은 동일한 집합에 속하게 되며, 최종적으로 연결 성분을 식별할 수 있습니다.
예시
그래프 G의 구성:
- 정점: {a, b, c, d, e, f}
- 간선: (a, b), (b, c), (c, d), (e, f)
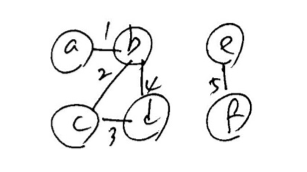

4. Same-Component 알고리즘

기능: 주어진 두 노드 u, v가 같은 연결 성분에 속하는지 확인합니다.
절차:
- find-set(u)와 find-set(v)의 결과를 비교합니다.
- 두 값이 같다면 같은 연결 성분에 속하므로 TRUE를 반환합니다.
- 다르면 FALSE를 반환합니다.
5. 응용: Prim's Algorithm과 Kruskal's Algorithm에서의 활용
- Prim's Algorithm:
- 최소 신장 트리(MST)에서 최소 우선순위 큐(Min Priority Queue)를 사용하여 노드를 선택합니다.
- 이 알고리즘은 탐욕적(Greedy) 접근법을 사용해 매번 최소 가중치 간선을 선택합니다.
- Kruskal's Algorithm:
- MST를 구할 때 Disjoint Set을 사용해 사이클을 방지하고, 연결된 성분을 관리합니다.
- 각 간선 (u, v)를 가중치 순서로 처리하며, 사이클이 생기지 않으면 union 연산으로 두 집합을 병합합니다.
6. Greedy Algorithm과 Disjoint Set의 역할
- 탐욕적 알고리즘(Greedy Algorithm):
- 최적의 해를 구하기 위해 매 순간 최선의 선택을 반복합니다.
- 예: Kruskal 알고리즘, Prim 알고리즘.
- 국소 최적화가 전역 최적화로 이어짐: 이 속성이 Prim과 Kruskal 알고리즘의 근간입니다.
- Disjoint Set은:
- Kruskal 알고리즘에서 간선 선택 시 사이클을 방지하는 데 사용됩니다.
- Prim 알고리즘에서는 최소 우선순위 큐(min-priority queue)를 사용하지만, Disjoint Set은 Kruskal 알고리즘에서 주로 사용됩니다
7. 요약
- Disjoint Set의 기본 연산
- make-set(v): 노드를 독립된 집합으로 초기화.
- find-set(x): 노드 x가 속한 집합의 대표자를 반환.
- union(x, y): 두 집합을 병합, 사이클 방지에 사용.
- Same-Component 알고리즘
- 두 노드가 같은 연결 성분에 속하는지 확인.
- find-set을 이용해 두 노드의 대표자가 같은지 비교.
- Prim's Algorithm : 최소 우선순위 큐를 이용해 탐욕적(Greedy)으로 최소 가중치 간선 선택.
- Kruskal's Algorithm: Disjoint Set으로 간선 선택 시 사이클을 방지
Reference
- Korea University - CVO101
'IT 일반 > 자료구조(개념) - [인강] 코드잇, [대학원] 전공 수업' 카테고리의 다른 글
| [대학원-자료구조 7~] Hash Table : an example of dictionary (0) | 2024.10.21 |
|---|---|
| [대학원-자료구조 6] MST : Kruskal's Alg., Prim's Alg. (1) | 2024.10.21 |
| [대학원-자료구조 4] Elementary Graph Algorithms : BFS, DFS (2) | 2024.10.20 |
| [대학원-자료구조 3] 기타 정렬 알고리즘 - MergeSort, QuickSort (1) | 2024.10.20 |
| [대학원-자료구조 1~2] Tree와 Graph, Heap (2) | 2024.10.19 |


