- 본 게시물에서는 간단하고, 이해하기 쉬우며, 가장 널리쓰이고, 비선형 모델에 쉽게 일반화될수 있으며, ML/DL의 근간이 되는 Linear Regression에 대해 알아본다.
- 사실 딥러닝도 Linear Regression만 제대로 이해하면 쉽게 이해할 수 있다고 하며, 의외로 AI 실무진들 중에서 Linear Regression에 대해 완벽히 설명할 수 있는 사람이 적다고 한다.
#1 AI/ML/DL 개요
AI/ML/DL 분류
- 시작된 시기와 각 분야별 커버하는 범위에 따라 분류

1) AI (Artificial Intelligence, 1950's ~)
- "A science like mathematics or biology."
- "It studies ways to build intelligent programs and machines that can creatively solve problems, which has always been considered a human prerogative(특권)"
2) ML (Machine Learning, 1980's ~)
- AI를 구현하는 방식에 대한 얘기로, 기계를 학습을 통해 intelligence를 갖게하는 일련의 행위
- "Machine Learning provides systems the ability to automatically learn and improve from experience without being explicitly programmed."
- "In ML, there are different algorithms (e.g. neural networks) that help to solve problems."
3) DL (Deep Learning, 2010's ~)
- 랜덤 포레스트, Nueral Network 등의 ML 기법들 중 특히 Nueral Network에 관한 분야
- "Deep Learning is a subset of machine learning, which uses the neural networks to analyze different factors with a structure that is similar to the human neural system."
- 2012년(한국 : 2015년)부로 핫해진 분야
Machine Learning
- 독립변수와 종속변수간의 Mapping Function을 찾는 과정
- Machine Learning Framework
1) Training : 주어진 Observed Data 중 가장 최적의 function을 고르는 과정
2) Testing : Learned Function을 활용하여 label 값들을 예측하는 과정
Deep Learning
- "Artificial Neural Networks that are composed of many layers"
- 다양한 ML 기법들로부터 얻어진 mapping function들 중 가장 best였던 방법론
(물론 ML 기법들 중 SVD는 아직 많이 쓰이고 있음)
Computer Vision
- "Science and Technology of Machines that See and Understand"
- 즉, 사람의 시각 지능을 모방하는 학문이며, Computer Science, Psychology, Biology, Physics, Engineering, Mathematics 분야와 모두 연관되어있음

#2 Linear Regression
Intro : Computer Vision에서의 Regression vs Classification

- 두번째 사진 : depth estimation을 의미하며 일종의 Regression 알고리즘을 활용
- 세번째 사진 : 각각의 개체를 분리시켜주는 segement estimaion을 의미하며, 비슷한 pixel들을 그룹핑시켜주는 일종의 Classification 알고리즘을 활용
Regression이란?
- 아래의 두 가지 목적(and/or)으로 input 변수와 output 변수들을 relate시키는 것
1) 새로운 input 변수들에대한 output 값들을 예측
2) output에 대한 input 값들의 효과를 이해
- 즉, input - output 사이의 mapping function을 찾는 과정
Regression에 활용되는 Dataset
1) 기본개념
- Regression에서는 아래와 같은 dataset pairs가 활용됨


- 물론, input 값으로는 스칼라값과 D dimension 벡터값 모두가 들어갈 수 있음
2) Input, Output 변수 동의어
- Input Variables : features, covariates, independent variables, explanatory variables, exogenous variables, predictors
- Output Variables : target, label, response, outcome, dependent variable, endogenous variables, measured variable
The Regression Function (Hypothesis)

- 'well enough' given inputs를 기반으로 output을 가장 잘 추정하는 mapping function을 찾으며, 이때의 function은 train data의 Xn과 Yn 사이의 상관관계를 가장 잘 설명하는 function이다.
- 즉, 우리는 위의 수식 중 f를 modeling 하는 것이 목적

- 위 그림에서 Learning Alorithm의 일종으로 Regression이 있는 것
Linear Regression
- Linear Regression : input과 output 사이에 linear relationship을 갖는다고 가정한 model이며, f()의 설계 관점에서 간단하다는 장점이 있음

Simple Linear Regression (단순 선형회귀)와 Learning
- Simple Linear Regression : 1개의 1차원 독립변수를 갖는 linear regression

- 위 f함수의 아래첨자 w = (w0,w1) : model의 2개의 parameter를 가리키며, 이 w벡터를 찾는게 modeling이다.
- 이 때의 w벡터들 중 가장 최적의 parameter w*를 찾는 과정을 learning(or estimating the parameters or fitting the model)이라고 하며, 이를위해 1) cost function과 2) optimization algorithm이 필요하다.
- (참고, ChatGPT(GPT4)) 위의 가중치 벡터는 추후 예측값을 계산할 때, input 벡터들과 dot product 시 활용되며, 이러한 가중치 벡터의 표현방식은 위와 같은 dot product를 통한 계산이 간단하게 수행되게 한다.

Learning Linear Regression
1) Learning
- Learning = Estimating the Parameters = Fitting the Model : 주어진 데이터로부터 최적의 parameter w*를 찾는 과정
→ 이를 위해 1) Cost Function 과 2) Optimization Algorithm이 필요
2) Learning의 아이디어


- 즉, 위 그림에서 실제 데이터 포인트들(빨간 점들)과 우리가 모델링한 fw(x)값과의 차이들을 최소화 시키는 w 벡터를 찾는 것이 Learning의 과정이고, 이를 식으로 표현하면 아래와 같다.

- 여기서 argmin은 argument of minimum의 약자로, argument는 ML에서 함수의 input값을 의미
- argmin w는 우측의 식을 최소화 하는 w 벡터를 찾는 과정 그 자체를 의미하며, 이게 Learning
- 우측의 식에서 제곱하고, 1/N을 한 이유는 리소스 관점에서의 practical한 이유로 minimum값만 찾으면 되니까 이 값 자체는 의미가 없음
- 우측의 식이 위의 예시에서는 MSE(Mean Squared Error)의 형태로 쓰였지만, 아래와 같이 일반화 시켜 나타낼 수도 있다.

- L(w)는 w에 관한 식으로(Cost Function), C는 위에서 fw(xn)와 yn에 대한 함수를 의미하며, 위의 예시에서는 제곱식이었음
- L(w) 값을 최소화시킨 벡터 w를 최적의 w 즉, w*라고 한다.
- (참고, ChatGPT(GPT4))위와 같은 최적화 과정을 나타내는 식은 기계학습 뿐만아니라 광범위한 범위에서 쓰일 수 있고, 그때마다 C 식와 W벡터의 형태들이 바뀔 수 있음
※ Loss Function과 Cost Function은 혼용해서 쓰이는 경우가 많으나, 통상적으로 Loss Function은 한 개의 데이터 포인트에서 나온 오차를 최소화하기 위해 정의되는 함수로, Cost Function은 위의 식처럼 모든 오차를 일반적으로 최소화하기 위해 정의되는 함수의 의미로 사용된다.
3) Linear Regression의 Design Choice
ⓐ Mapping Function 설계
ⓑ Cost Function 설계
ⓒ Optimiztion 설계
Cost Function
- Cost Function (= energy, loss, training objective)은 데이터를 잘 설명하는 parameters W를 학습하는 데 사용되며, 우리가 모델링한 모델이 얼마나 데이터를 잘 설명하는 지를 quantify한다.
1) Cost Function Intuition1

- 우선 w0 = 0 고정인 경우에 w값과 이에 따른 L(w)값을 graph로 표현해본다.

- w1이 각각 1,1/2, 0 일때의 L(w) 값을 표현해보면 위 사진의 오른쪽 빨간색 그래프의 세개의 data point처럼 나타낼 수 있고, 이를 모든 w1에 대하여 graph를 그려보면 위와 같은 2차함수 형태의 Cost Curve가 나온다고 한다.
※ 위 강의노트 캡처본은 w1이 0일 때의 fw(x) 그래프 (좌측)과 이에 따른 L(w) 값을 계산하는 과정이 필기되어 있음
2) Cost Function Intuition2

- 1) Cost Function Intuition1에서 w0=0으로 고정시켰는데, 본절에서는 w0까지 고려하는 것으로 확장시켜 본다.

- 위의 예시에서는 w0 와 w1을 각각 50과 0.06으로 가정했을 때의 fw(x)와 이에 따른 L(w)를 나타내고 있는데, 여기서의 L(w)는 w0와 w1에 대한 함수이므로, 이를 graph로 나타내면 3차원이 되게 된다.

- 위의 예시에서 우측 data point는 절편이 800, 기울기가 -0.03일 때의 L(w)값을 나타내며 우리는 가장 낮은 L(w) 값을 나타낼때의 parameter vector w*를 찾아야 하는 게 목표이다.
- 위의 우측 그래프에서는 L(w)값의 높낮이를 색깔로 나타냈는데, 이는 실제로는 아래와 같은 형태를 띈다.

3) 좋은 Cost Function이 가져야하는 조건
ⓐ 0에 대해 symmetric
- 특정 부호(양수/음수) 위주로 최적화할 경우 bias가 발생
ⓑ Large mistake와 very large mistake를 비슷하게 봐야된다.
- 즉, 아래 그림에서 빨간색 데이터 포인트들에 대한 회귀식을 1번보다는 outlier 2개에 대한 에러(large error, very large error)를 비슷하게 여긴 2번으로 산출해내는 Cost Function이 바람직 하다는 의미

4) MSE, MAE : 대표적인 Cost Function
- Cost Function을 활용하여 Mapping Function을 구할 때, Statistical Property와 computal 연산 및 리소스 사용 측면에선의 Computal cost 간에는 trade-off 관계가 있음
- MSE와 MAE가 연산이 간단하면서 0에 대해 Symmetric하기 때문에 가장 대표적인 Cost Function으로 사용되며, 여전히 outlier에는 영향을 많이 받는다는 한계점이 있음
- 연산량이 많지만 large mistake와 very large mistake를 비슷하게 보는 이상적인 cost function으로는 huber loss 등이 있음
ⓐ MSE(Mean Squared Error)
- 가장 대중적으로 많이 쓰이는 Cost Function
- 위에서 설명한 statistical property와 computal cost 간의 trade-off 관계에서 가장 현실적으로 많은 경우들의 니즈를 충족한 cost function

ⓑ MAE(Mean Absolute Error)

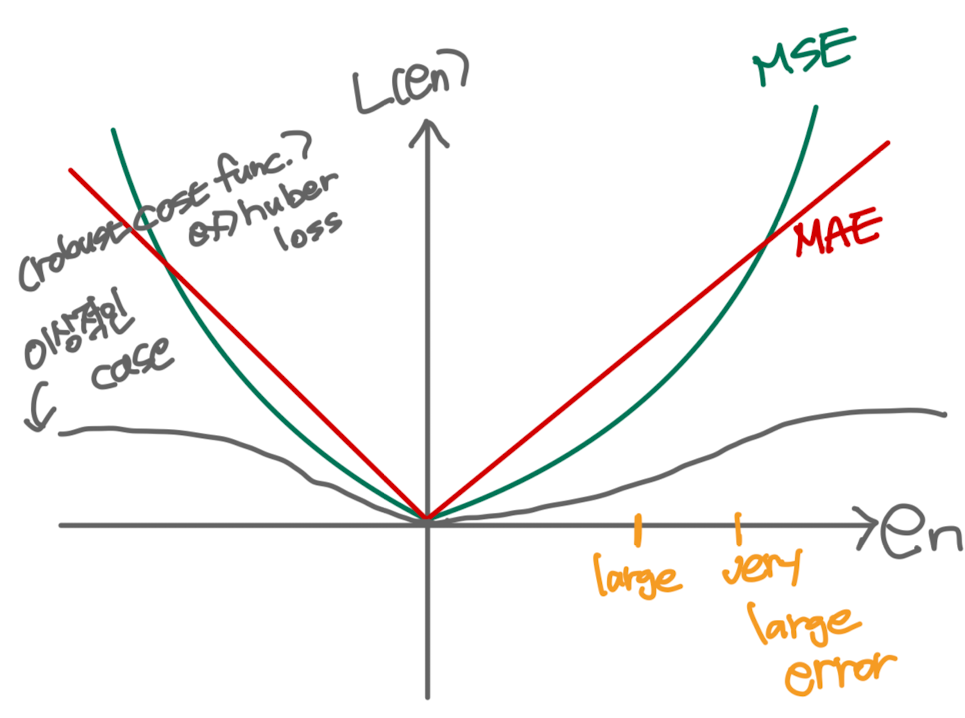
※ 물론, 실제 cost function에 활용될 때에는 위에 두 개의 식으로 표현된 en^2값 뿐만 아니라 n으로 나눠주는 과정까지 포함되어야 하며, 엄밀히 말해서는 1/n까지 붙어야 MSE, MAE라고 할 수 있음
# References
- Deep Learning by I.Goodfellow et al.
- Dive into Deep Learning by A.Zhang et al.
- nvidiablog
- Korea Univ. AAI107, 'Machine Learning' Lecture
'기계학습 > ML,DL Backgroud 이론 - [대학원] 전공 수업' 카테고리의 다른 글
| [기계학습 11~12] 5. Convolutional Neural Networks (CNNs) - 작성 중 (1) | 2024.06.08 |
|---|---|
| [기계학습 8~10] 4. Neural Network and Backpropagation (2) - 작성 중 (0) | 2024.06.07 |
| [기계학습 7] 4. Neural Network and Backpropagation (1) (0) | 2024.05.04 |
| [기계학습 4] Classification(Logistic Regression) - 작성중 (0) | 2024.04.13 |
| [기계학습 3] Optimization, Multivariate Linear Regression(다변량 선형 회귀) (2) | 2024.04.13 |



