- 본 게시물에서는 [기계학습 1~2] 게시물에서 지속적으로 언급됐던 Mapping Function Fw(Xn)의 파라미터 벡터 w 중 최적의 값을 찾아나가는 Optimazation 과정에 대해 상술
# Optimization
Cost Function L(w)에 대해 아래와 같은 최적의 w벡터를 찾고자 함

# Grid Search : Optimazation 방식 1
- brute-force한 방식이지만 가장 간단한 방식으로, grid 내의 모든 w 값에 대한 cost를 연산한 후 가장 최적의 w 값을 선택한다.
- 그러나, 'foor loops'가 너무 많으며, 이에따라 exponential computational complexity를 초래한다.

# Gradient Descent(경사 하강법) : Optimazation 방식 2
1) INTRO
- Gradient Descent : 아래의 세 가지 값이 변함에 따라 달라지는 w벡터 중 최적의 w벡터를 찾는 방식
ⓐ Where Start? : initialization data point
ⓑ Which Direction? : negative gradient
ⓒ How much Move ? : learning rate

2) Gradient
- Gradient (at a point) : 한 데이터 포인트에서의 function에 대한 접선의 기울기(the slope of the tangent)로, 이는 해당 함수의 가장 큰 증가 방향을 가리킨다.(?)
- Gradient Descent 알고리즘의 방향은 'negative gradient'로 해당 데이터포인트에서의 접선의 기울기에 '-'를 붙인 값이다.
- 아래의 그림에서 2,3차원에서의 데이터 포인트별 negative gradient 방향을 기하학적으로 확인할 수 있다.


3) Gradient Descent 과정
ⓐ initialization data point w = (w0, w1) 에서부터 시작
ⓑ ⓐ에서의 data point로부터 negative gradient 방향으로 이동하여 또 다른 데이터포인트 w' = (w0', w1')로 이동함으로써 L(w)값을 줄이며, 이러한 과정을 반복하여 최종적으로 minimum L(w)값을 찾아 optimal w 벡터를 찾는다.
이를 기하학적으로 나타내면 아래와 같다.


위의 과정을 수식으로 나타내면 아래와 같으며, w0와 w1을 계속 update하는 과정으로 convergence(수렴)할 때 까지 반복한다.

이를 일반화시키면 아래와 같고, 노란색 하이라이팅된 부분이 같은 것을 의미한다.

※ 이를 코드로 구현한다면 for 또는 while문으로 구현된다.
※ parameter : model이 산출, hyper parameter : 사람이 지정
4) Properties of Gradient Descent
(gradient의 부호에 따른 특성)
당연하지만, w 값의 접선의 기울기의 부호에 따라 update 되는 negative gradient 방향이 다르다.
예를들어,

위와 같은 w1 update 수식에서 하이라이팅된 부분을 아래와 같이 두 가지 케이스로 나누어 기하학적으로 표현한다면 아래와 같다.


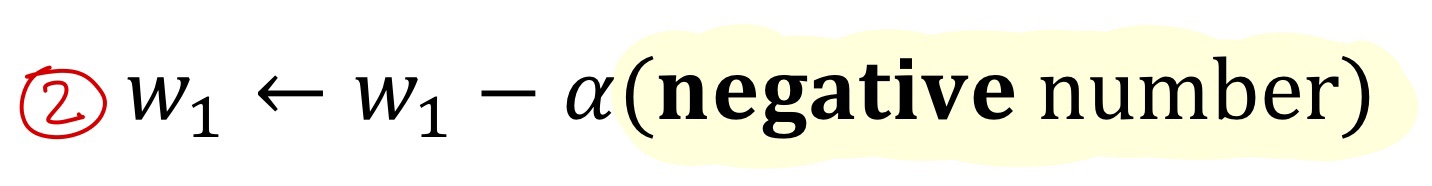

(하이퍼파라미터인 learning rate에 대한 특성)
- learning rate 값은 '얼만큼 움직일지'에 대한 값이므로, too small 하다면, gradient descent값이 slow하게 움직이고, too large하다면 minumum을 지나쳐버릴 수 있다. 즉, converge하는 데 실패하거나 diverge 해버릴 수도 있다.
- 단, 불행히도 learning rate를 어떻게 설정할 지에 대한 것은 정답이 없어서, 우리는 그저 proper learning rate를 설정해야 된다.
5) Gradient Descent의 한계

- 어쩔 수 없이, L(w)의 편미분값이 0이 되어 버리면 update되는 w값이 converge해서 update를 멈추므로, 위와 같이 Global minumum이 아니라 local munimal에 빠질 수 있음
# Multivariate Linear Regression(다변량 선형 회귀)
1) Multivariate Linear Regression 개요
- 2개 이상의 독립변수를 활용하여 하나 이상의 종속 변수(반응 변수)의 값을 예측하는 선형 회귀 모델로, 우선 본 게시물에서는 종속변수를 한 개의 스칼라 값으로 가정하여 상술한다.
2) Multivariate Linear Regression 공식
- 독립변수 벡터 Xn들과 이들의 coefficient이자, Model의 parameter들인 W 벡터를 내적한 것이 회귀식 또는 Mapping Function Fw(Xn)이며, 이를 수식으로 나타내면 아래와 같다.
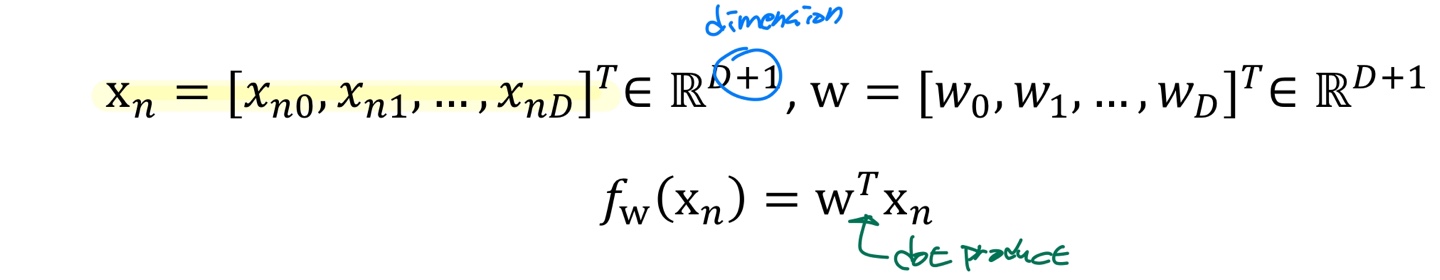
- 즉, 우리의 목표는 회귀 모델링을 통해 위의 식 기준으로 D+1개의 parameter w를 찾는 것이다.
- 보다 직관적인 이해를 위해, dimension을 5로, Xn0값을 1로 가정하고 Mapping Function을 늘여서 쓴다면 아래와 같다.

3) Gradient Descent for Multivariate Linear Regression
- 단순 선형회귀 때와 마찬가지로 각각의 w값에 대하여 편미분을 해줘야 하며, 이를 보다 일반화 하여 나타내면 아래와 같다.

(과제1 풀이)

# Reference
- Deep Learning by I.Goodfellow et al.
- Dive into Deep Learning by A.Zhang et al.
- Korea Univ. AAI107, 'Machine Learning' Lecture
'기계학습 > ML,DL Backgroud 이론 - [대학원] 전공 수업' 카테고리의 다른 글
| [기계학습 11~12] 5. Convolutional Neural Networks (CNNs) - 작성 중 (1) | 2024.06.08 |
|---|---|
| [기계학습 8~10] 4. Neural Network and Backpropagation (2) - 작성 중 (0) | 2024.06.07 |
| [기계학습 7] 4. Neural Network and Backpropagation (1) (0) | 2024.05.04 |
| [기계학습 4] Classification(Logistic Regression) - 작성중 (0) | 2024.04.13 |
| [기계학습 1~2] AI/ML/DL 및 Linear Regression 개요, Cost Function (0) | 2024.03.16 |



